ATE, ATT, CATE, Bias : 실무로 통하는 인과추론 학습기(1)

딥다이브, 실무로 통하는 인과추론 스터디 그룹에서 학습하며 과제로 작성된 글 입니다.

[1주차 과제] 잠재적 결과

해당 데이터는 튜터링이 성적에 얼마나 영향을 미치는지 확인하기 위해, 1000명의 학생의 성적을 생성한 가상 결과입니다. 이 데이터는 체계적으로 편향되어 있고, 전지적인 능력으로 잠재적 결과(Potential Outcome)를 모두 알고 있다고 가정합니다. 이번 과제의 목표는 ATE, ATT, CATE 등 다양한 개념을 익히는 것입니다.

과제 가이드

1. 주어진 데이터를 기반으로 실제 ATE, ATT CATE를 계산합니다. CATE에 들어가는 조건은 FinancialStatus입니다.
2. 관찰 가능한 데이터를 추출하고, 잘못된 방법으로 ATE를 추정해봅니다.

3. 관찰 가능한 데이터로 ATE를 추정하고 싶었지만, 주어진 데이터에는 편향(Bias)이 반영되어 있습니다.
   
   E[Y | T=1] - E[Y | T=0]
= E[Y_1 | T=1] - E[Y_0 | T=0] + E[Y_0 | T=1] - E[Y_0 | T=0]

   이중 E[Y_0 | T=1] - E[Y_0 | T=0] 이 편향을 의미합니다.
   이 편향한 뒤, ATT에 더해 잘못된 ATE가 어떻게 계산되는지 확인해봅니다.

4. 실제 Tutoring의 효과를 측정하기 위해, 새롭게 Tutoring 여부를 랜덤 할당합니다. 컬럼명은 RandomTutoring으로 설정해주세요.
5. 실제 ATE 값과 비교해 RandomTutoring한 뒤 다시 ATE를 추정해봅니다.

데이터 로드

먼저 학습에 필요한 데이터를 불러왔습니다. 이 데이터프레임은 학생들의 튜터링 전후 점수와 관련된 정보를 담고 있습니다.

1. StudentID: 학생의 고유 식별자.
2. PreTutoringScore: 튜터링 이전의 학생 점수.
3. PostTutoringScore: 튜터링 이후의 학생 점수.
4. Tutoring: 학생이 튜터링을 받았는지 여부를 나타내는 이진 변수 (1은 튜터링을 받은 것을 나타냄).
5. PotentialOutcomeTreated: 튜터링을 받은 경우의 잠재적 결과 점수.
6. PotentialOutcomeControl: 튜터링을 받지 않은 경우의 잠재적 결과 점수.
7. FinancialStatus: 학생의 금융적 상태를 나타내는 범주형 변수 (높음, 중간, 낮음).

import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

file_path = "./"
file_name = 'week_1_potential_outcome_tutoring_effect.csv'
df = pd.read_csv(os.path.join(file_path, file_name)); df

데이터 프레임에 대한 기초 정보

데이터 프레임에 대한 기초 정보를 조회해 보았습니다. 결측치는 존재하지 않았습니다.

df.info()

범주형 ‘FinancialStatus’

FinancialStatus 의 범주별로 등장 횟수를 세어 보았습니다.

• “Medium” 금융 상태를 가진 학생은 482명입니다.
• “High” 금융 상태를 가진 학생은 319명입니다.
• “Low” 금융 상태를 가진 학생은 199명입니다.

df['FinancialStatus'].value_counts()

데이터 프레임에 대한 기초 통계량

기초 통계량을 조회해 보았습니다.

df.describe()

관측 가능한 데이터

우리가 A라는 학생에게 대해서 실제 관측 가능한 데이터는 A 학생이 튜터링을 받았을 때 튜더링 받은 후 성적입니다. A가 튜터링을 받은 순간 우리는 A가 튜터링을 받지 않았을 때의 잠재적 결과 점수를 알 수 없습니다. 반대로 A가 튜터링을 받지 않았을 때 튜더링을 받을 경우의 잠재적 결과 점수를 알 수 없습니다. 때문에 모든 상황에서 관측 가능한 데이터는 StudentID, PreTutoringScore, PostTutoringScore, Tutoring, FinancialStatus입니다.

여기에서는 observed_df로 PreTutoringScore, PostTutoringScore, Tutoring만 추출했다.

observed_df = df[['PreTutoringScore','PostTutoringScore', 'Tutoring']].copy(); observed_df

관측 가능한 데이터에 한정해 봤을 때, 체계적으로 편향되어 있습니다.

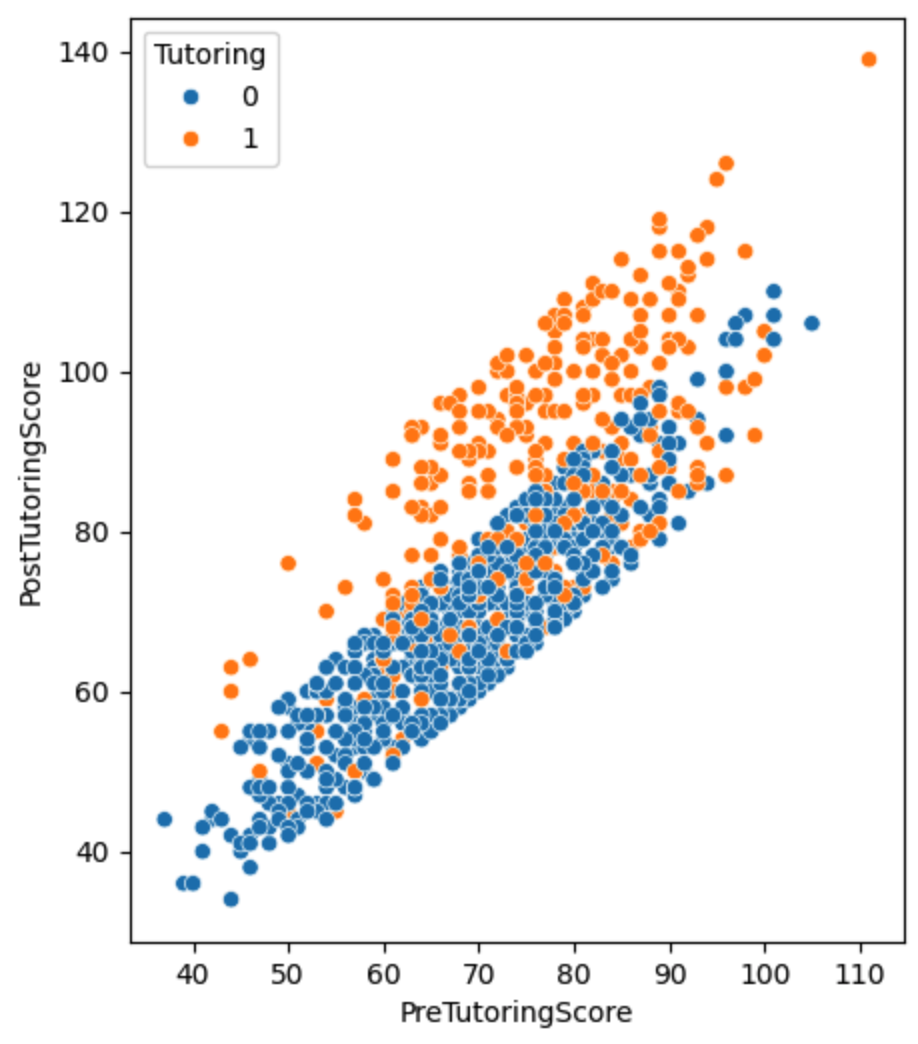
각 점은 한 학생을 나타내며, x축은 튜터링 전의 점수(PreTutoringScore), y축은 튜터링 후의 점수(PostTutoringScore)를 나타냅니다. 그래프를 보았을 때 전반적으로 튜터링을 받은 학생들의 점수 향상이 큰 것을 확인 할 수 있습니다.

plt.figure(figsize=(5, 6), dpi = 100)
sns.scatterplot(x = 'PreTutoringScore', y = 'PostTutoringScore', data = observed_df, hue = 'Tutoring')
plt.show()

관측 가능한 (편향) 데이터로 추정한 ATE

평균 처치 효과(Average Treatment Effect)는 다음과 같은 3개로 연산 가능합니다.

• ATE = E[τi​]
• ATE = E[Yi1] - E[Yi0]
• ATE = E[Y|T=1] - E[Y|T=0]

각 기호의 의미는 다음과 같습니다.

• ATE : Average Treatment Effect (평균 처리 효과)
• τi ​: Yi1​−Yi0​
• Yi1 : Treatment Group의 결과
• Yi0 : Control Group의 결과
• Y|T=1 : 처리를 받은 경우의 결과
• Y|T=0 : 처리를 받지 않은 경우의 결과

Yi1, Yi0, τi은 모든 데이터 행에 대하여 관측할 수 없습니다. 관측 가능한 데이터 observed_df를 만들었을 때의 값으로 계산 가능한 ATE = E[Y|T=1] - E[Y|T=0]을 활용하여 ATE를 추정해 보았습니다.

gap(인과 추정량) = PostTutoringScore - PreTutoringScore

# 관측 가능한 (편향) 데이터로 추정한 ATE (단, 이 경우에는 observed_df에서 계산하세요.)
observed_df['gap'] = observed_df['PostTutoringScore'] - observed_df['PreTutoringScore']

# Tutoring 그룹과 Non-Tutoring 그룹의 변화 평균 계산
treated = observed_df[observed_df['Tutoring'] == 1]
control = observed_df[observed_df['Tutoring'] == 0]

treated_mean_change = treated['gap'].mean()
control_mean_change = control['gap'].mean()

# ATE 계산
biased_ate = treated_mean_change - control_mean_change

print(f'관측 가능한 데이터로 추정한 평균 처치 효과 (ATE): {biased_ate:.4f}')

실제 ATE (Average Treatment Effect) 계산

실제 ATE는 ATE = E[τi​]로 연산했습니다.

ate = (df['PotentialOutcomeTreated'] - df['PotentialOutcomeControl']).mean()

print(f"올바른 평균 처치 효과 (ATE): {ate:.4f}")

ATT (Average Treatment Effect on the treated) 계산

실험군에 대한 평균처치효과(Average Treatment Effect on the treated)는 다음과 같이 연산 가능합니다.

• ATE = E[Yi1 - Yi0 | T=1]

Tutoring이 1인 데이터를 선별한 뒤 PotentialOutcomeTreated와 PotentialOutcomeControl의 차이를 평균냈습니다.

Treated_df = df[df["Tutoring"] == 1]

att = (Treated_df['PotentialOutcomeTreated'] - Treated_df['PotentialOutcomeControl']).mean()

print(f"튜터링 그룹에 대한 평균 처치 효과 (ATT): {att:.4f}")

실제 CATE (Conditional Average Treatment Effect) 계산

조건부 평균처치효과(Conditional Average Treatment Effect)는 다음과 같이 연산 가능합니다. 이는 변수 X로 정의된 그룹에서의 처치효과를 추출할 수 있다.

• ATE = E[Yi1 - Yi0 | X=x]

FinancialStatus을 그룹별로 구분한뒤 각 항목에 대한 평균값을 구했습니다.

df['gap'] = df['PotentialOutcomeTreated'] - df['PotentialOutcomeControl']

grouped_ate = df.groupby('FinancialStatus')['gap'].mean()

high_cate = grouped_ate["High"]
medium_cate = grouped_ate["Medium"]
low_cate = grouped_ate["Low"]

print(f"경제력이 높은 조건에 대한 CATE (CATE): {high_cate:.4f}")
print(f"경제력이 중간인 조건에 대한 CATE (CATE): {medium_cate:.4f}")
print(f"경제력이 낮은 조건에 대한 CATE (CATE): {low_cate:.4f}")

편향

편향계산식

1️⃣ E[Y | T=1] - E[Y | T=0]
2️⃣ = E[Y1 | T=1] - E[Y0 | T=0]
3️⃣ = E[Y1 | T=1] - E[Y0 | T=0] + E[Y0 | T=1] - E[Y0 | T=1]
4️⃣ = E[Y1 - Y0 | T=1] + { E[Y0 | T=1] - E[Y0 | T=0] }
5️⃣ = ATT + { E[Y0 | T=1] - E[Y0 | T=0] }
❗️ 편향 = { E[Y0 | T=1] - E[Y0 | T=0] }

설명

1️⃣ 먼저 평균처리효과에 대한 식 입니다.
2️⃣ T가 1일 때 Y에 대하여도 Y1만 관측 가능하고 T가 0일때 Y는 0만 관측 가능하기 때문에 다음과 같은 식이 성립됩니다.
3️⃣ 해당 식에 동일한 항인 E[Y0 | T=1]을 더하고 뺍니다.
4️⃣ 식을 정리하면 위와 같이 표현 가능합니다.
5️⃣ 식에서 E[Y1 - Y0 | T=1]에서 ATT로 표현가능합니다.
❗️ 처치를 받을 대상과 처치를 받지 않을 대상이 동일하면 테스트 환경에 차이가 없습니다. 즉, 최종적으로 { E[Y0 | T=1] - E[Y0 | T=0] }이 0이라면 편향이 없음을 의미합니다.

때문에 먼저 Tutoring의 여부에 따라 데이터프레임을 나누고 각각의 PotentialOutcomeControl의 차이를 구했습니다.

Treated_df = df[df["Tutoring"] == 1]
Not_Treated_df = df[df["Tutoring"] == 0]

bias = Treated_df["PotentialOutcomeControl"].mean() - Not_Treated_df["PotentialOutcomeControl"].mean()

print(f"편향: {bias:.4f}")

Biased ATE가 계산된 이유

Biased ATE의 경우 위에서 본 편향의 수식과 같이 Att + bias로 연산가능합니다.

new_biased_ate = att + bias
print(f'편향된 ATE를 다르게 계산한 결과: {new_biased_ate:.4f}')

가상의 데이터(df)에 랜덤 튜터링(RandomTutoring) 할당 (np.random.binomial)

df 데이터 프레임에 랜덤 튜터링 RandomTutoring 컬럼을 추가하였습니다. 추가된 값은 0 또는 1이며, 각 값이 나올 확률은 0.5로 설정했습니다.

df['RandomTutoring'] = np.random.binomial(n=1, p=0.5, size=1000)

랜덤 튜터링을 할당한 후, ATT 계산

RandomTutoring을 활용하여 ATT를 계산해보았습니다.

Treated_df = df[df["RandomTutoring"] == 1]

random_att = (Treated_df['PotentialOutcomeTreated'] - Treated_df['PotentialOutcomeControl']).mean()

print(f"랜덤 튜터링 그룹에 대한 평균 처치 효과 (ATT): {random_att:.4f}")

랜덤 튜터링을 할당한 후, 편향 계산

RandomTutoring을 활용하여 편항을 계산해보았습니다.

Treated_df = df[df["RandomTutoring"] == 1]
Not_Treated_df = df[df["RandomTutoring"] == 0]

random_bias = Treated_df["PotentialOutcomeControl"].mean() - Not_Treated_df["PotentialOutcomeControl"].mean()

print(f"랜덤 튜터링 그룹에 대한 편향: {random_bias:.4f}")

랜덤 튜터링을 할당한 후, 다시 추정된 ATE 계산

RandomTutoring을 활용하여 ATE를 계산해 보았습니다.

df['gap'] = df['PostTutoringScore'] - df['PreTutoringScore']

# RandomTutoring 그룹과 Non-RandomTutoring 그룹의 변화 평균 계산
Treated_df = df[df["RandomTutoring"] == 1]
Not_Treated_df = df[df["RandomTutoring"] == 0]

treated_mean_change = Treated_df['gap'].mean()
control_mean_change = Not_Treated_df['gap'].mean()

# ATE 계산
random_ate = treated_mean_change - control_mean_change

new_random_ate = random_att + random_bias

print(f"랜덤 튜터링 그룹 할당 후 추정한 ATE: {random_ate:.4f}")
print(f"랜덤 튜터링 그룹 할당 후 다른 방법으로 추정한 ATE: {new_random_ate:.4f}")

랜덤화로 얻을 수 있는 것

처리를 무작위로 할당함으로써 실험 그룹 간의 차이가 외부 요인에 의해 인한 것인지 처리의 결과인지 판단할 수 있습니다.

Written by 유찬영

youngchannel4u@gmail.com