선형 회귀 | 프리슈-워-로벨 정리 | 더미 변수 : 실무로 통하는 인과추론 학습기(2)


딥다이브, 실무로 통하는 인과추론 스터디 그룹에서 학습하며 과제로 작성된 글 입니다.
해당 데이터는 수면 시간이 성적에 얼마나 영향을 미치는지 확인하기 위해, 10000명의 학생의 성적을 생성한 가상 결과입니다. 이번 과제의 목표는 선형 회귀, 프리슈-워-로벨 정리, 더미 변수에 대하여 다양한 개념을 익히는 것입니다.
과제 가이드
데이터 속 교란을 일으키는 컬럼을 회기분석 보정 방법으로 찾아냅니다.
프리슈-워-로벨 정리와 직교화를 활용하여 편향제거, 잡음제거, 결과모델 단계를 수행합니다. 최종적으로 결과 모델으로 ATE를 구합니다.
더미 변수를 활용한 회귀 모델 분석하기
컬럼 설명
Family_Support : 학생의 집에서의 지원 정도
Study_Hours : 학생의 공부 시간
Tutoring_Hours : 과외 시간
Sleep_Hours : 수면 시간
Grade : 학생의 성적
먼저 학습에 필요한 데이터를 로드했습니다.
import numpy as np
import pandas as pd
import statsmodels.formula.api as smf
from matplotlib import pyplot as plt
import seaborn as sns
data = pd.read_csv('student_grades.csv')
| Family_Support | Study_Hours | Tutoring_Hours | Grade | Sleep_Hours | |
|---|---|---|---|---|---|
| 0 | 4.641325 | 1.451124 | 0.883172 | 92.028017 | 12.082951 |
| 1 | 3.447945 | 1.164094 | 0.473210 | 66.682681 | 12.505711 |
| 2 | 3.546153 | 1.297287 | 0.000000 | 54.858793 | 11.928777 |
| 3 | 4.285227 | 1.815799 | 1.015303 | 100.000000 | 12.045285 |
| 4 | 3.998437 | 2.353050 | 1.923918 | 100.000000 | 12.358695 |
| ... | ... | ... | ... | ... | ... |
| 9995 | 5.304515 | 2.076668 | 1.375749 | 100.000000 | 12.028399 |
| 9996 | 4.281873 | 1.586581 | 0.000000 | 65.249884 | 12.044210 |
| 9997 | 3.165458 | 1.445638 | 0.000000 | 54.401417 | 12.296208 |
| 9998 | 6.404860 | 2.163024 | 1.904617 | 100.000000 | 12.132608 |
| 9999 | 5.042470 | 2.235757 | 2.272015 | 100.000000 | 12.757906 |
10000 rows × 5 columns
먼저 수면시간이 성적에 어떤 영향을 미치는지에 대한 단순 선형회귀를 실시합니다. 선형 회귀의 결과 값은 수면시간과 성적은 음의 상관관계를 갖는다고 나타납니다.
formula = 'Grade ~ Sleep_Hours'
model = smf.ols(formula, data=data).fit()
model.summary().tables[1]
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 99.2817 | 3.515 | 28.243 | 0.000 | 92.391 | 106.172 |
| Sleep_Hours | -0.5202 | 0.292 | -1.783 | 0.075 | -1.092 | 0.052 |
진짜 수면을 적게 할 수록 성적이 좋아질까? 검증을 해야합니다. 일차적으로는 수면시간 외에 공부시간, 과외시간, 집에서의 지원 정도를 포함하여 선형회귀 모델을 다시 만들어 봅니다. 놀랍게도 수면시간과 성적은 양의 상관관계를 갖게 됩니다. 이렇게 단순 데이터 사이의 상관관계는 어떤 데이터를 고려하는지에 따라 달라 질 수 있다는 점을 알 수 있었습니다.
formula = 'Grade ~ Sleep_Hours+Tutoring_Hours+Study_Hours+Family_Support'
model = smf.ols(formula, data=data).fit()
model.summary().tables[1]
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 48.8462 | 2.578 | 18.947 | 0.000 | 43.793 | 53.900 |
| Sleep_Hours | 0.5941 | 0.208 | 2.855 | 0.004 | 0.186 | 1.002 |
| Tutoring_Hours | 7.8357 | 0.179 | 43.711 | 0.000 | 7.484 | 8.187 |
| Study_Hours | 6.2127 | 0.217 | 28.666 | 0.000 | 5.788 | 6.638 |
| Family_Support | 3.3037 | 0.152 | 21.686 | 0.000 | 3.005 | 3.602 |
편향 제거 단계
# 회귀 모델을 생성하고 데이터에 적합시킵니다.
debiasing_model = smf.ols('Sleep_Hours ~ Family_Support + Study_Hours + Tutoring_Hours', data = data).fit()
debiasing_model.resid + data['Sleep_Hours'].mean()
처치인 Sleep_Hours에 대하여 나머지 교란 요인들을 통제하는 과정입니다. 해당 변수들도 Sleep_Hours에 영향을 미치는 변수인 만큼, 그 영향력을 제거하겠다는 의미입니다. 이렇게 통제하고 나면 잔차(교란 변인들로 설명되지 않는 차이)에 따라(즉, 순수한 Sleep_Hours의 차이에 따라) 결과를 예측할 수 있을 것입니다.
# 회귀 모델의 잔차(residuals)와 평균을 더하여 sleep_hours_res 열을 생성합니다.
data_deb = data.assign(
sleep_hours_res = (debiasing_model.resid + data['Sleep_Hours'].mean()))
# Sleep_Hours에 대한 편향제거된 회귀모델
model_w_deb_data = smf.ols('Grade ~ sleep_hours_res', data = data_deb).fit()
print(model_w_deb_data.summary().tables[1])
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -4.086e-14 | 0.007 | -5.91e-12 | 1.000 | -0.014 | 0.014 |
| sleep_hours_res | 1.0000 | 0.001 | 1741.657 | 0.000 | 0.999 | 1.001 |
그래서 이 차이만 가지고도 결과 Grade에 대해 회귀했을 때 앞서 계산한 회귀 분석 결과와 동일한 회귀 계수(0.5941)를 얻을 수 있습니다. 모든 교란 요인을 통제하여 불편 추정량을 얻은 것입니다.
하지만, 표준편차가 크고 P값 역시 상대적으로 크게 나타납니다. 결과에 잡음을 제거하여 분산을 줄여 볼 수 있습니다.
잡음 제거 단계
# Grade에 대한 잡음제거
denoising_model = smf.ols(
'Grade ~ Family_Support + Study_Hours + Tutoring_Hours', data = data).fit()
data_denoise = data_deb.assign(
grade_res=denoising_model.resid + data_deb["Grade"].mean())
잡음을 제거하고 해당 결과를 data_denoise에 할당했습니다.
#표준오차 Family_Support + Tutoring_Hours + Study_Hours 세 변수 활용
model_se = smf.ols(
'Grade ~ Family_Support + Tutoring_Hours + Study_Hours', data = data).fit()
print("SE regression:", model_se.bse["Family_Support"])
>>> SE regression: 0.15239839952386264
model_family_support_aux = smf.ols(
'Family_Support ~ Tutoring_Hours + Study_Hours', data = data
).fit()
# subtract the degrees of freedom - 4 model parameters - from N.
se_formula = (np.std(model_se.resid)
/(np.std(model_family_support_aux.resid)*np.sqrt(len(data)-4)))
print("SE formula: ", se_formula)
>>> SE formula: 0.15239839952386258
두 결과는 각기 다른 식으로 SE(표준 오차)를 계산하는 방법을 알려줍니다
이 두 개념은 회귀 분석 및 통계적 추정에서 중요한 역할을 하며, 데이터 분석에서 모델의 정확성과 신뢰도를 평가하는 데 필수적입니다.
표준 오차 (SE) 회귀는 회귀 분석에서 예측 값과 실제 값 간의 차이를 측정하는 중요한 통계량입니다. 이는 모델이 얼마나 잘 데이터를 설명하고 있는지 평가하는 데 사용됩니다.
공식:
회귀의 표준 오차(SE regression) 또는 표준 추정 오차(standard error of estimate)는 다음과 같이 계산됩니다:
[ SE_{regression} = \sqrt{\frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{n - k - 1}} ]
여기서:
의미:
표준 오차(SE)는 표본 통계량의 변동성을 측정하는 데 사용되는 통계량입니다. 이는 표본 평균과 모집단 평균 사이의 차이를 추정하는 데 사용됩니다.
공식:
표본 평균의 표준 오차(SE)는 다음과 같이 계산됩니다:
[ SE = \frac{s}{\sqrt{n}} ]
여기서:
의미:
결과 모델 단계
최종적으로 결과 잔차와 처치 잔차를 활용해 처치효과를 추정합니다.
# Grade, sleep_hours_res 활용한 최종모델
model_w_orthogonal = smf.ols('grade_res ~ sleep_hours_res', data = data_denoise).fit()
print(model_w_orthogonal.summary().tables[1])
모델의 정보를 출력해 봅니다.
print(model_w_orthogonal.summary())
OLS Regression Results
==============================================================================
Dep. Variable: Grade R-squared: 0.000
Model: OLS Adj. R-squared: 0.000
Method: Least Squares F-statistic: 4.132
Date: Wed, 22 May 2024 Prob (F-statistic): 0.0421
Time: 00:16:07 Log-Likelihood: -41173.
No. Observations: 10000 AIC: 8.235e+04
Df Residuals: 9998 BIC: 8.236e+04
Df Model: 1
Covariance Type: nonrobust
===================================================================================
coef std err t P>|t| [0.025 0.975]
-----------------------------------------------------------------------------------
Intercept 85.8705 3.521 24.389 0.000 78.969 92.772
sleep_hours_res 0.5941 0.292 2.033 0.042 0.021 1.167
==============================================================================
Omnibus: 5282.850 Durbin-Watson: 2.010
Prob(Omnibus): 0.000 Jarque-Bera (JB): 31173.610
Skew: -2.581 Prob(JB): 0.00
Kurtosis: 9.941 Cond. No. 287.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
회귀 계수를 사용하여 ATE를 구할 수 있었습니다.
# ATE는 T의 계수로부터 추정
ATE = model_w_orthogonal.params['sleep_hours_res']
print('ATE:', ATE)
ATE: 0.5941159185740237
# Study_Hours 값을 10개의 구간으로 나눕니다
data['Study_Hours_Bin'] = pd.cut(data['Study_Hours'], bins=10, labels=False)
data
data['Study_Hours_Bin'].value_counts()
Study_Hours의 Bin이 고르지 않게 나타납니다. Study_Hours는 어느 정도 정규분포를 나타내는 것으로 보이는데요, 그래서인지 양끝으로 갈수록 Bin의 수가 줄어듭니다.
이는 조건부로 계산했을 때 단순히 평균을 내는 것이 아니라, 가중치를 부여해야 한다는 것을 알려주기도 하죠.
Study_Hours_Bin
3 2671
4 2640
2 1600
5 1572
1 626
6 573
0 158
7 140
8 16
9 4
Name: count, dtype: int64
plt.figure(figsize=(15,6))
sns.histplot(data=data,
x="Study_Hours",
hue="Study_Hours_Bin")
plt.title("Conditional random experiment")
plt.show()
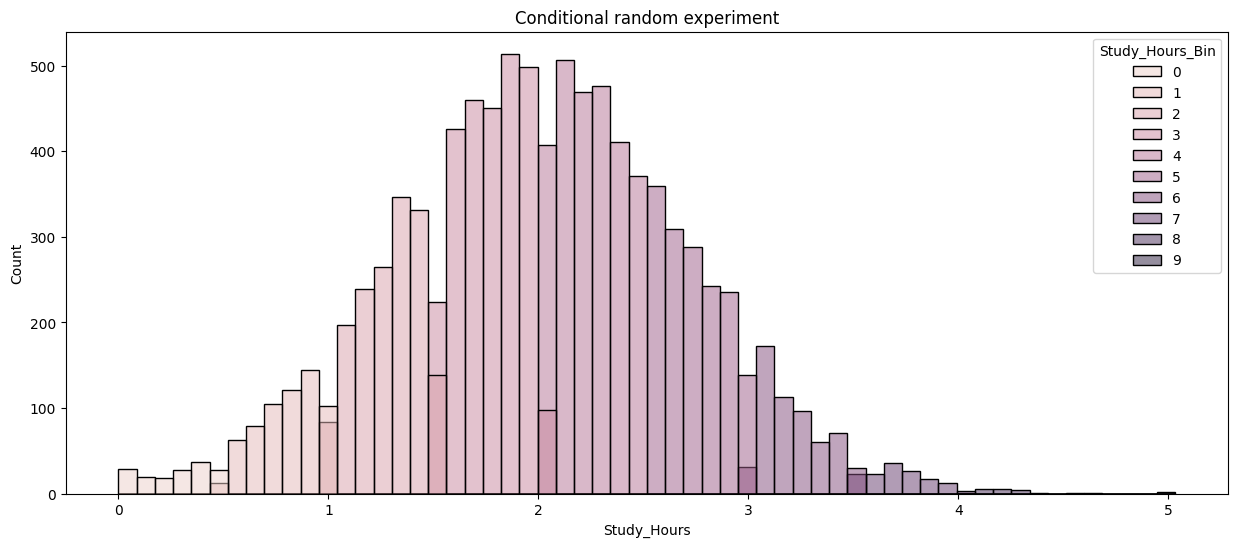
Study_Hours 의 분포를 나타내면 위와 같습니다.
data_dummies = (data
.join(pd.get_dummies(data["Study_Hours_Bin"],
prefix="sb",
drop_first=True)))
data_dummies.head()
| Family_Support | Study_Hours | Tutoring_Hours | Grade | ... | sb_6 | sb_7 | sb_8 | sb_9 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 4.641325 | 1.451124 | 0.883172 | 92.028017 | ... | False | False | False | False |
| 1 | 3.447945 | 1.164094 | 0.473210 | 66.682681 | ... | False | False | False | False |
| 2 | 3.546153 | 1.297287 | 0.000000 | 54.858793 | ... | False | False | False | False |
| 3 | 4.285227 | 1.815799 | 1.015303 | 100.000000 | ... | False | False | False | False |
| 4 | 3.998437 | 2.353050 | 1.923918 | 100.000000 | ... | False | False | False | False |
5 rows × 15 columns
sb_1부터 sb_9까지의 변수들이 각각 더미 변수로서 회귀 모델에 표함된다. 모든 머디 변수를 회귀식에 직접 포함시키기 때문에 이 방식은 Sleep_Hours와 함께 Grade를 설명하는 독립 변수로 사용된다.
model = smf.ols(
"Grade ~ Sleep_Hours + sb_1+sb_2+sb_3+sb_4+sb_5+sb_6+sb_7+sb_8+sb_9",
data=data_dummies
).fit()
model.summary().tables[1]
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 48.4990 | 2.689 | 18.039 | 0.000 | 43.229 | 53.769 |
| sb_1[T.True] | 19.5741 | 0.963 | 20.331 | 0.000 | 17.687 | 21.461 |
| sb_2[T.True] | 35.2175 | 0.902 | 39.044 | 0.000 | 33.449 | 36.986 |
| sb_3[T.True] | 46.2975 | 0.885 | 52.293 | 0.000 | 44.562 | 48.033 |
| sb_4[T.True] | 50.2937 | 0.886 | 56.791 | 0.000 | 48.558 | 52.030 |
| sb_5[T.True] | 51.1733 | 0.902 | 56.712 | 0.000 | 49.405 | 52.942 |
| sb_6[T.True] | 51.2733 | 0.972 | 52.773 | 0.000 | 49.369 | 53.178 |
| sb_7[T.True] | 51.2859 | 1.255 | 40.866 | 0.000 | 48.826 | 53.746 |
| sb_8[T.True] | 51.2867 | 2.837 | 18.081 | 0.000 | 45.727 | 56.847 |
| sb_9[T.True] | 51.2817 | 5.474 | 9.368 | 0.000 | 40.551 | 62.012 |
| Sleep_Hours | 0.0179 | 0.213 | 0.084 | 0.933 | -0.399 | 0.435 |
두 번째 방식의 경우 Study_Hours_Bin 변수를 범주형 변수로 간주하고 자동으로 더미 변수로 변환해 회귀 모델에 포함시켰다.
model = smf.ols("Grade ~ Sleep_Hours + C(Study_Hours_Bin)",
data=data).fit()
model.summary().tables[1]
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 48.4990 | 2.689 | 18.039 | 0.000 | 43.229 | 53.769 |
| C(Study_Hours_Bin)[T.1] | 19.5741 | 0.963 | 20.331 | 0.000 | 17.687 | 21.461 |
| C(Study_Hours_Bin)[T.2] | 35.2175 | 0.902 | 39.044 | 0.000 | 33.449 | 36.986 |
| C(Study_Hours_Bin)[T.3] | 46.2975 | 0.885 | 52.293 | 0.000 | 44.562 | 48.033 |
| C(Study_Hours_Bin)[T.4] | 50.2937 | 0.886 | 56.791 | 0.000 | 48.558 | 52.030 |
| C(Study_Hours_Bin)[T.5] | 51.1733 | 0.902 | 56.712 | 0.000 | 49.405 | 52.942 |
| C(Study_Hours_Bin)[T.6] | 51.2733 | 0.972 | 52.773 | 0.000 | 49.369 | 53.178 |
| C(Study_Hours_Bin)[T.7] | 51.2859 | 1.255 | 40.866 | 0.000 | 48.826 | 53.746 |
| C(Study_Hours_Bin)[T.8] | 51.2867 | 2.837 | 18.081 | 0.000 | 45.727 | 56.847 |
| C(Study_Hours_Bin)[T.9] | 51.2817 | 5.474 | 9.368 | 0.000 | 40.551 | 62.012 |
| Sleep_Hours | 0.0179 | 0.213 | 0.084 | 0.933 | -0.399 | 0.435 |
더미변수를 활용해 분석한 결과, 수면 시간과 성적의 관계가 음에서 양으로 바뀌었다. 이를 통해 더미 변수 활용으로 교란 요인을 통제했다는 것을 확인 할 수 있다. 이전 모델에 비해 수면 시간의 계수의 절댓값이 매우 작아졌는데, 교란 요인을 통제하니 전체 집단에 대해서는 수면시간과 성적 간 관계가 미미하게 나타난다. 때문에 그룹별로 살펴볼 필요가 있다.
def regress(df, t, y):
return round(smf.ols(f'{y} ~ {t}', data = df).fit().params[t], 6)
effect_by_group = data_dummies.groupby('Study_Hours_Bin').apply(regress, y = 'Grade', t = 'Sleep_Hours')
effect_by_group
>>>
Study_Hours_Bin
0 9.015105
1 6.002520
2 0.747068
3 -1.999126
4 -0.464798
5 -0.066598
6 -0.019569
7 -0.000000
8 -0.000000
9 0.000000
dtype: float64
공부 시간의 급간을 일종의 조건부(Condition)으로 본다면, 0번 / 1번 그룹에서 수면 시간(Sleep Hours)과 Grade 관계는 비교적 강한 상관 계수를 가지고 있다. 반면 다른 구간에 대해서는 거의 상관성이 나타나지 않는다. 구간에 대해 편차가 큰 만큼, 결과에 대해 의미 있는 해석이 가능하다.
이 결과를 해석한다면, 공부 시간이 적은 경우 수면을 많이 취할수록 성적이 크게 향상되고, 공부 시간이 많아질수록 수면 시간 자체는 크게 영향을 미치지 않는 것으로 보인다.
이런 경향성은 더미 변수 4~9번 그룹에서 더욱 크게 드러나는데, 이는 해당 그룹이 Grade에 미치는 회귀 계수에서도 알 수 있다. 해당 그룹은 약 50~51 정도의 계수를 가지고 있는데, 이는 각 집단이 포함하고 있는 특성으로 성적에 미치는 영향력을 많이 설명할 수 있다는 것과 같다. 그중 수면 시간은 미미한 영향력을 끼치고 있다.
댓글