성향 점수 : 실무로 통하는 인과추론 학습기(3)


딥다이브, 실무로 통하는 인과추론 스터디 그룹에서 학습하며 과제로 작성된 글 입니다.
해당 데이터는 NGO의 구호활동이 영아사망률에 미치는 영향을 알아보기 위해 생성한 가상의 결과입니다. 이번 과제의 목표는 회귀, 성향점수 매칭, 역확률 가중치 등 여러 추정 방식이 어떠한 상황에서 적절한지 알아보는 것입니다.
과제 가이드
주어진 데이터를 기반으로 회귀, 성향점수 추정, 성향점수 매칭, 역확률 가중치 방식을 활용해 ATE를 추정합니다.
각 추정 값을 비교합니다.
어떤 추정 방식이 적합한지 확인해봅니다.
컬럼 설명
intervention: 구호활동 (처치변수)
Infant_Mortality_Rate: 영아사망률
Poverty_Level: 가난정도
Doctor_Ratio : 의사비율
—
먼저 필요한 패키지를 참조하고 패키지의 기본적인 출력 설정을 조정했습니다.
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import graphviz as gr
from matplotlib import style
import seaborn as sns
from matplotlib import pyplot as plt
style.use("ggplot")
import statsmodels.formula.api as smf
import matplotlib
from cycler import cycler
color=['0.2', '0.6', '1.0']
default_cycler = (cycler(color=color))
linestyle=['-', '--', ':', '-.']
marker=['o', 'v', 'd', 'p']
plt.rc('axes', prop_cycle=default_cycler)
데이터를 로드 후 기본적인 정보를 조회해 보았습니다.
df = pd.read_csv('data.csv')
df.describe()
| Intervention | Infant_Mortality_Rate | Poverty_Level | Doctor_Ratio | |
|---|---|---|---|---|
| count | 100.000000 | 100.000000 | 100.000000 | 100.000000 |
| mean | 0.470000 | 0.529871 | 49.989196 | 5.073747 |
| std | 0.501614 | 0.266197 | 9.129294 | 2.194726 |
| min | 0.000000 | 0.088320 | 30.124311 | -1.482535 |
| 25% | 0.000000 | 0.330700 | 42.948723 | 3.518037 |
| 50% | 0.000000 | 0.432600 | 50.778050 | 5.122489 |
| 75% | 1.000000 | 0.786500 | 54.836915 | 6.362527 |
| max | 1.000000 | 0.998200 | 74.632421 | 12.705463 |
기본적으로 처치 변수만을 활용해 회귀식을 얻었습니다. 변수의 P-value 값으로 보았을 때 유의미한 관계임을 알 수 있었습니다.
#처치변수만을 넣은 회귀식
import statsmodels.formula.api as smf
formula = "Infant_Mortality_Rate ~ Intervention"
smf.ols(formula,
data=df).fit().summary().tables[1]
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 0.7155 | 0.025 | 29.155 | 0.000 | 0.667 | 0.764 |
| Intervention | -0.3950 | 0.036 | -11.034 | 0.000 | -0.466 | -0.324 |
그 외 교란 변수를 모두 넣은 회귀식 입니다. 처치의 계수에 큰 편차가 없어보입니다.
#그외 교란변수를 모두 넣은 회귀식
model = smf.ols("Infant_Mortality_Rate ~ Intervention + Poverty_Level + Doctor_Ratio", data=df).fit()
model.summary().tables[1]
print("ATE:", model.params['Intervention'])
print("95% CI:", model.conf_int().loc["Intervention", :].values.T)
ATE: -0.3925015635619009 95% CI: [-0.46385031 -0.32115282]
이 과정은 Poverty_Level과 Doctor_Ratio를 사용하여 Intervention이 발생할 확률을 추정하는 로지스틱 회귀 모델을 적합시킵니다. 성향 점수는 개입 효과를 추정할 때 혼란 변수를 통제하기 위한 중요한 도구입니다.
1️⃣ 우리가 추정하고자 하는 목표 값은 ‘Intervention’이라는 특정 처치가 ‘Infant_Mortality_Rate’(영아사망률)에 미치는 영향
2️⃣ 이때 ‘Intervention’ 외에도 ‘Poverty_Level’이나 ‘Doctor_Ratio’와 같은 다른 변수들도 ‘Infant_Mortality_Rate’에 영향을 미침[공변량(Covariates) = Poverty_Level and Doctor_Ratio]
3️⃣ 성향점수(Propensity Score)는 이런 공변량들이 주어졌을 때, ‘Intervention’이 발생할 확률을 나타내는 값
4️⃣ 즉, ‘Intervention’에 대한 공변량의 성향점수를 계산하는 것은, 공변량의 영향력을 통제하고 ‘Intervention’의 순수한 효과를 추정하기 위한 방법
이 균형점수는 종종 처치의 조건부 확률(P(T|X))이나 성향점수(e(x))라고 부릅니다.
Intervention입니다. = TPoverty_Level과 Doctor_Ratio입니다. = X#성향점수 e(x) 추정
ps_model = smf.logit("Intervention ~ Poverty_Level + Doctor_Ratio", data=df).fit(disp=0)
예측된 상향점수 값
data_ps = df.assign(
propensity_score = ps_model.predict(df),
)
data_ps[["Intervention", "Infant_Mortality_Rate", "propensity_score"]].head()
| Intervention | Infant_Mortality_Rate | propensity_score | |
|---|---|---|---|
| 0 | 0 | 0.8909 | 0.464727 |
| 1 | 1 | 0.3432 | 0.473603 |
| 2 | 1 | 0.3122 | 0.467047 |
| 3 | 1 | 0.2324 | 0.559505 |
| 4 | 0 | 0.7999 | 0.476754 |
처치변수 개입 여부에 따른 성향점수의 분포 확인해보기
sns.histplot(data=data_ps, x='propensity_score', hue='Intervention', element='step', stat='density', common_norm=False)
plt.title('성향점수의 분포에 따른 처치변수 개입 여부')
plt.xlabel('성향점수')
plt.ylabel('밀도')
plt.show()
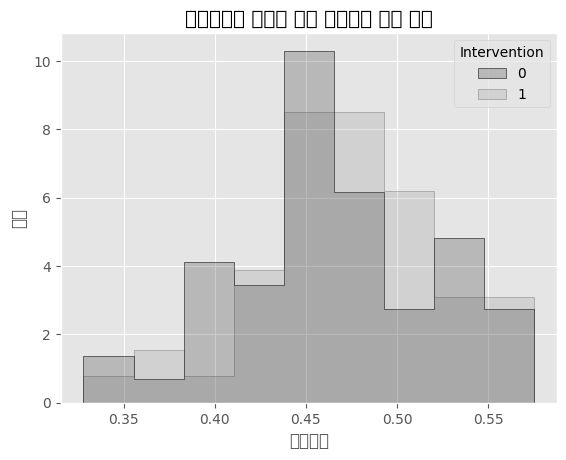
| 선형회귀도 성향점수 추정과 매우 비슷하며, 편향 제거 단계에서 E[T | X]를 추정합니다 |
교란 요인 X를 보정하기위해 성향점수를 활용하였습니다.
성향 점수(Propensity Score)를 사용하여 개입 효과(Average Treatment Effect, ATE)를 추정하는 과정을 보여줍니다. Intervention의 처치효과가 커진 것을 확인 할 수 있었습니다.
model = smf.ols("Infant_Mortality_Rate ~ Intervention + propensity_score",
data=data_ps).fit()
print("ATE:", model.params['Intervention'])
ATE: -0.39248271937192675
성향점수를 통제하는 또 다른 접근 방식은 매칭 추정량 matching estimator입니다.
이 방법은 관측 가능한 특징이 비슷한 실험 대상의 짝을 찾아 실험군과 대조군을 비교합니다.
먼저, 성향점수를 유일한 특성으로 사용하여 실험군에 KNN 모델을 적합시키고 대조군의 Y1을 대체하는 데 사용합니다.
다음으로, 대조군에 KNN 모델을 적합시키고 실험군의 Y0을 대체합니다.
두 경우 모두 대체된 값은 성향점수에 기반하여 매칭된 실험 대상의 결과죠.
from sklearn.neighbors import KNeighborsRegressor
T = "Intervention"
X = "propensity_score"
Y = "Infant_Mortality_Rate"
treated = data_ps.query(f"{T}==1")
untreated = data_ps.query(f"{T}==0")
mt0 = KNeighborsRegressor(n_neighbors=1).fit(untreated[[X]],
untreated[Y])
mt1 = KNeighborsRegressor(n_neighbors=1).fit(treated[[X]], treated[Y])
predicted = pd.concat([
# find matches for the treated looking at the untreated knn model
treated.assign(match=mt0.predict(treated[[X]])),
# find matches for the untreated looking at the treated knn model
untreated.assign(match=mt1.predict(untreated[[X]]))
])
predicted.head()
| Intervention | Infant_Mortality_Rate | Poverty_Level | Doctor_Ratio | propensity_score | match | |
|---|---|---|---|---|---|---|
| 1 | 1 | 0.3432 | 47.009926 | 7.907068 | 0.473603 | 0.7999 |
| 2 | 1 | 0.3122 | 50.917608 | 4.470686 | 0.467047 | 0.7865 |
| 3 | 1 | 0.2324 | 30.124311 | 10.440338 | 0.559505 | 0.7865 |
| 7 | 1 | 0.1320 | 44.817298 | 5.964945 | 0.495428 | 0.7345 |
| 8 | 1 | 0.2432 | 41.915064 | 4.553074 | 0.518903 | 0.7865 |
차이 계산: (predicted[Y] - predicted["match"])
실제 결과(Y)와 매칭된 결과(match)의 차이
(predicted[Y] - predicted["match"])*predicted[T]
이 부분은 처리가 있는 경우(T=1)에만 차이를 고려, predicted[T]가 1일 때만 이 차이가 더함
처치가 된 집단에서는 처치된 결과값 - 처치가 안됐을때 값 predicted["match"] 를 뺌
(predicted["match"] - predicted[Y])*(1-predicted[T])
이 부분은 처리가 없는 경우(T=0)에만 차이를 고려, 1 - predicted[T]가 1일 때만 이 차이가 더함
처치가 안된 집단에서는 처치된 결과값 predicted["match"] - 처치가 안됐을때 값을 뺌
즉 둘다 가정으로 처치가 됐을때 - 처치가 안됐을 때 값으로 처치 값 연산
두 경우의 차이 합산:(predicted[Y] - predicted["match"])*predicted[T] + (predicted["match"] - predicted[Y])*(1-predicted[T])
두 경우의 차이를 모두 합산한 결과입니다.
평균 계산: np.mean(...)
모든 데이터 포인트에 대해 계산된 차이의 평균을 구합니다.
#성향점수 매칭 결과로 얻는 ATE
match_ATE = np.mean((predicted[Y] - predicted["match"])*predicted[T]
+ (predicted["match"] - predicted[Y])*(1-predicted[T]))
print("ATE:", match_ATE)
ATE: -0.356096
관측된 각 사례를 그 사례가 선택될 확률의 역수로 가중치를 부여함으로써, 모집단 전체를 대표하도록 샘플을 조정합니다.
IPW의 기본 원리는 다음과 같습니다:
이를 통해, 처치 확률이 매우 낮은 경우(예: 드문 처치를 받은 경우)에는 해당 데이터 포인트에 높은 가중치를 부여하게 됩니다. 이 과정은 처치 집단과 비처치 집단 간의 차이를 보정하여, 마치 모든 대상이 무작위로 처치를 받은 것처럼 만듭니다
assign: 새로운 열을 추가합니다.
weight: 처치 여부에 따라 가중치를 계산합니다.
propensity_score: 성향 점수를 소수점 둘째 자리까지 반올림합니다.groupby: 성향 점수와 처치 여부별로 데이터를 그룹화합니다.
mean(): 각 그룹의 평균 가중치와 평균 유아 사망률을 계산합니다.reset_index(): 그룹화된 데이터를 평탄화하여 데이터프레임으로 만듭니다g_data = (data_ps
.assign(
weight = data_ps["Intervention"]/data_ps["propensity_score"] + (1-data_ps["Intervention"])/(1-data_ps["propensity_score"]),
propensity_score=data_ps["propensity_score"].round(2)
)
.groupby(["propensity_score", "Intervention"])
[["weight", "Infant_Mortality_Rate"]]
.mean()
.reset_index())
plt.figure(figsize=(10,4))
for t in [0, 1]:
sns.scatterplot(data=g_data.query(f"Intervention=={t}"), y="Infant_Mortality_Rate", x="propensity_score", size="weight",
sizes=(1,100), color=color[t], legend=None, label=f"T={t}", marker=marker[t])
plt.title("Inverse Probability of Treatment Weighting")
plt.legend()
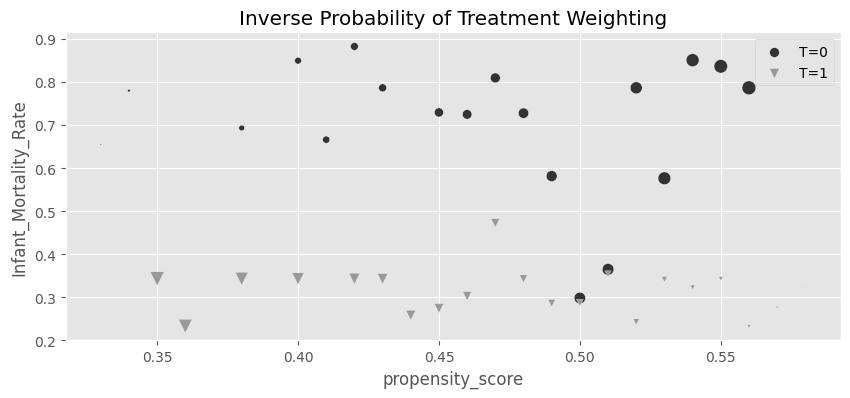
처치군과 비처치군 각각에 대한 가중 평균을 구한 후 ATE를 계산합니다
weight_t: 처치군의 가중치 = 1 / 성향 점수weight_nt: 비처치군의 가중치 = 1 / (1 - 성향 점수)t1: 처치군의 유아 사망률t0: 비처치군의 유아 사망률y1: 처치군의 가중 평균 유아 사망률y0: 비처치군의 가중 평균 유아 사망률y1 - y0모호한 집단에 결과값에 대하여 예민 반응을 한다?….
weight_t = 1/data_ps.query("Intervention==1")["propensity_score"]
weight_nt = 1/(1-data_ps.query("Intervention==0")["propensity_score"])
t1 = data_ps.query("Intervention==1")["Infant_Mortality_Rate"]
t0 = data_ps.query("Intervention==0")["Infant_Mortality_Rate"]
y1 = sum(t1*weight_t)/len(data_ps)
y0 = sum(t0*weight_nt)/len(data_ps)
print("E[Y1]:", y1)
print("E[Y0]:", y0)
print("ATE", y1 - y0)
E[Y1]: 0.3205342619875382 E[Y0]: 0.7138347022578627 ATE -0.3933004402703245
IPW 공식을 직접 적용하여 데이터 전체에서 ATE를 계산
(data_ps["Intervention"] - data_ps["propensity_score"]): 처치 여부에서 성향 점수를 뺀 값
data_ps["propensity_score"] * (1 - data_ps["propensity_score"]): 성향 점수와 그 보수의 곱#역확률 가중치로 얻는 ATE
IPW_ATE = np.mean(data_ps["Infant_Mortality_Rate"]
* (data_ps["Intervention"] - data_ps["propensity_score"])
/ (data_ps["propensity_score"]*(1-data_ps["propensity_score"])))
print("ATE:",IPW_ATE)
ATE: -0.3933004402703245
dmatrix(ps_formula, df)를 사용하여 설계 행렬 X를 생성합니다. 여기서 ps_formula는 처치 확률을 예측하기 위한 공식을 나타내며, df는 데이터프레임입니다.
XX
LogisticRegression 모델을 사용하여 처치 확률을 추정합니다. penalty="none"은 규제 항이 없음을 의미하며, max_iter=1000은 최대 반복 횟수를 설정합니다. 이 모델을 X와 처치 변수 df[T]에 적합시켜 처치 확률을 추정합니다.predict_proba 메서드를 사용하여 수행되며, 결과에서 처치 확률 (클래스 1의 확률)만을 선택합니다.(df[T] - ps) / (ps * (1 - ps)) * df[Y]를 사용하여 가중치를 부여한 결과 변수를 계산합니다. 여기서 df[T]는 처치 변수, ps는 예측된 처치 확률, df[Y]는 결과 변수입니다.np.mean을 사용하여 수행됩니다.from sklearn.linear_model import LogisticRegression
from patsy import dmatrix
# define function that computes the IPW estimator
def est_ate_with_ps(df, ps_formula, T, Y):
X = dmatrix(ps_formula, df)
ps_model = LogisticRegression(penalty="none",
max_iter=1000).fit(X, df[T])
ps = ps_model.predict_proba(X)[:, 1]
# compute the ATE
return np.mean((df[T]-ps) / (ps*(1-ps)) * df[Y])
formula = """Poverty_Level + Doctor_Ratio"""
T = "Intervention"
Y = "Infant_Mortality_Rate"
est_ate_with_ps(df, formula, T, Y)
>>> - 0.3933004355383178
부트스트랩을 사용하여 ATE의 95% 신뢰 구간을 계산하고 출력
from joblib import Parallel, delayed # for parallel processing
def bootstrap(data, est_fn, rounds=200, seed=123, pcts=[2.5, 97.5]):
np.random.seed(seed)
stats = Parallel(n_jobs=4)(
delayed(est_fn)(data.sample(frac=1, replace=True))
for _ in range(rounds)
)
return np.percentile(stats, pcts)
from toolz import partial
print(f"ATE: {est_ate_with_ps(df, formula, T, Y)}")
est_fn = partial(est_ate_with_ps, ps_formula=formula, T=T, Y=Y)
print(f"95% C.I.: ", bootstrap(df, est_fn))
ATE: -0.3933004355383178 95% C.I.: [-0.45442286 -0.31455193]
print("Original Sample Size", data_ps.shape[0])
print("Treated Pseudo-Population Sample Size", sum(weight_t))
print("Untreated Pseudo-Population Sample Size", sum(weight_nt))
>>> Original Sample Size 100
>>> Treated Pseudo-Population Sample Size 99.96699061739257
>>> Untreated Pseudo-Population Sample Size 100.02045315052773
p_of_t는 데이터프레임 data_ps에서 처치 변수 Intervention의 평균값을 계산합니다. 이는 전체 데이터에서 처치를 받을 확률의 평균을 의미합니다.t1은 처치를 받은 샘플만 포함하는 데이터프레임을 생성합니다 (Intervention == 1).t0은 처치를 받지 않은 샘플만 포함하는 데이터프레임을 생성합니다 (Intervention == 0).weight_t_stable는 처치를 받은 샘플에 대한 가중치를 계산합니다. 이는 전체에서 처치를 받을 확률을 각 샘플의 성향 점수로 나누어 계산됩니다.weight_nt_stable는 처치를 받지 않은 샘플에 대한 가중치를 계산합니다. 이는 전체에서 처치를 받지 않을 확률을 각 샘플의 성향 점수의 보수(1에서 뺀 값)로 나누어 계산됩니다.p_of_t = data_ps["Intervention"].mean()
t1 = data_ps.query("Intervention==1")
t0 = data_ps.query("Intervention==0")
weight_t_stable = p_of_t/t1["propensity_score"]
weight_nt_stable = (1-p_of_t)/(1-t0["propensity_score"])
print("Treat size:", len(t1))
print("W treat", sum(weight_t_stable))
print("Control size:", len(t0))
print("W treat", sum(weight_nt_stable))
nt는 처치를 받은 그룹의 샘플 수입니다.nc는 처치를 받지 않은 그룹의 샘플 수입니다.y1은 처치를 받은 그룹에서 Infant_Mortality_Rate (유아 사망률)의 가중 평균입니다.t1["Infant_Mortality_Rate"]*weight_t_stable는 각 샘플의 유아 사망률과 해당 샘플의 가중치를 곱한 값입니다.sum(t1["Infant_Mortality_Rate"]*weight_t_stable)는 이 값을 모두 더한 것입니다.sum(t1["Infant_Mortality_Rate"]*weight_t_stable)/nt는 전체 가중치를 샘플 수로 나누어 가중 평균을 계산합니다.y0은 처치를 받지 않은 그룹에서 Infant_Mortality_Rate (유아 사망률)의 가중 평균입니다.y1과 유사하며, weight_nt_stable를 사용하여 가중 평균을 계산합니다.ATE는 처치를 받은 그룹의 가중 평균 유아 사망률 (y1)과 처치를 받지 않은 그룹의 가중 평균 유아 사망률 (y0)의 차이입니다.print("ATE: ", y1 - y0)는 ATE 값을 출력합니다.nt = len(t1)
nc = len(t0)
y1 = sum(t1["Infant_Mortality_Rate"]*weight_t_stable)/nt
y0 = sum(t0["Infant_Mortality_Rate"]*weight_nt_stable)/nc
print("ATE: ", y1 - y0)
# 그래프 설정
plt.figure(figsize=(14, 7))
# 히스토그램 및 KDE 설정
sns.histplot(data=df, x='Infant_Mortality_Rate', hue='Intervention', kde=True, element='step', stat="density", common_norm=False, palette='viridis', bins=10)
# 그래프 제목과 레이블 설정
plt.title('Distribution of Infant Mortality Rate by Intervention', fontsize=16)
plt.xlabel('Infant Mortality Rate', fontsize=14)
plt.ylabel('Density', fontsize=14)
plt.legend(title='Intervention', labels=['No Intervention', 'Intervention'])
# 그래프 출력
plt.show()
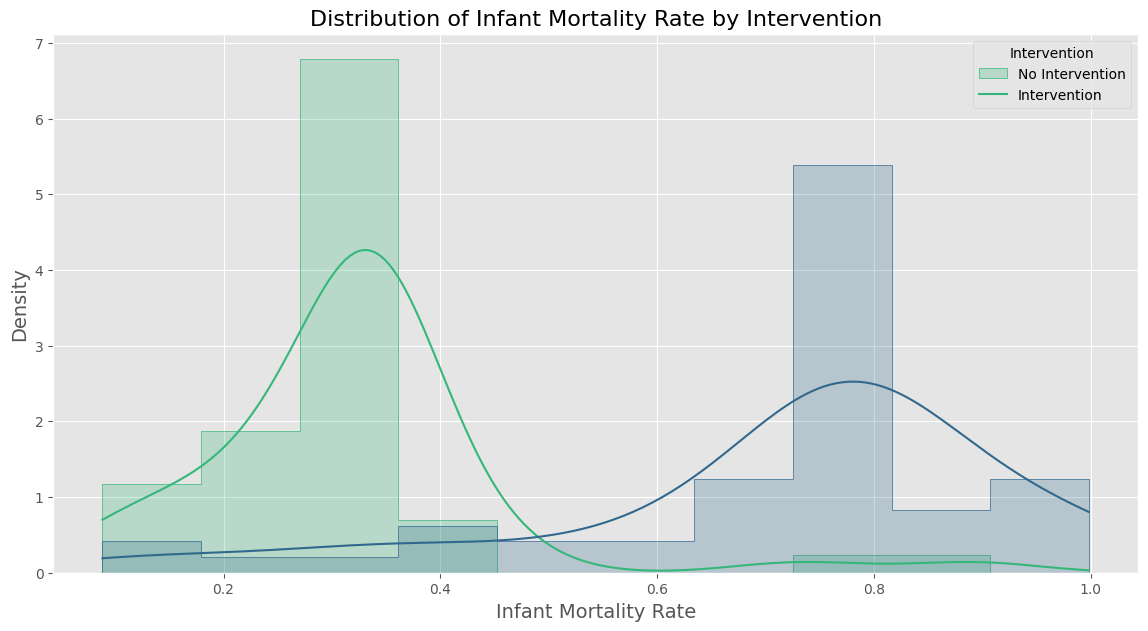
저의 경우 특정 행 2번 줄 처치된 실험군의 이상치를 만들었습니다.
# df.head()에서 파악한 head의 특정 행의 Infant_Mortality_Rate 임의로 바꾸기
# 처치를 했을 때(실험군)의 'Infant_Mortality_Rate'를 바꿔봐도 되고, 처치를 안했을 때(대조군)의 'Infant_Mortality_Rate'를 바꿔봐도 됩니다!
df.at[2, 'Infant_Mortality_Rate'] = 0.98
처치 변수의 처치값이 줄어든 것을 확인할 수 있었습니다.
#처치변수만을 넣은 회귀식
import statsmodels.formula.api as smf
formula = "Infant_Mortality_Rate ~ Intervention"
smf.ols(formula,
data=df).fit().summary().tables[1]
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 0.7155 | 0.026 | 27.354 | 0.000 | 0.664 | 0.767 |
| Intervention | -0.3808 | 0.038 | -9.980 | 0.000 | -0.457 | -0.305 |
평균 처치 값도 줄어든 것을 확인 할 수 있었습니다.
#그외 교란변수를 모두 넣은 회귀식
model = smf.ols("Infant_Mortality_Rate ~ Intervention + Poverty_Level + Doctor_Ratio", data=df).fit()
model.summary().tables[1]
print("ATE:", model.params['Intervention'])
print("95% CI:", model.conf_int().loc["Intervention", :].values.T)
ATE: -0.37806445933642996 95% CI: [-0.45408231 -0.30204661]
동일하게 성향점수를 추정했습니다.
ps_model = smf.logit("Intervention ~ Poverty_Level + Doctor_Ratio", *data*=df).fit(*disp*=0)
data_ps = df.assign(
propensity_score = ps_model.predict(df),
)
data_ps[["Intervention", "Infant_Mortality_Rate", "propensity_score"]].head()
| Intervention | Infant_Mortality_Rate | propensity_score | |
|---|---|---|---|
| 0 | 0 | 0.8909 | 0.464727 |
| 1 | 1 | 0.3432 | 0.473603 |
| 2 | 1 | 0.9800 | 0.467047 |
| 3 | 1 | 0.2324 | 0.559505 |
| 4 | 0 | 0.7999 | 0.476754 |
성향점수를 활용한 직교화로 ATE를 연산했습니다
model = smf.ols("Infant_Mortality_Rate ~ Intervention + propensity_score",
data=data_ps).fit()
print("ATE:", model.params['Intervention'])
ATE: -0.37803529386191914
동일하게 성향점수 매칭도 진행했습니다.
from sklearn.neighbors import KNeighborsRegressor
T = "Intervention"
X = "propensity_score"
Y = "Infant_Mortality_Rate"
treated = data_ps.query(f"{T}==1")
untreated = data_ps.query(f"{T}==0")
mt0 = KNeighborsRegressor(n_neighbors=1).fit(untreated[[X]],
untreated[Y])
mt1 = KNeighborsRegressor(n_neighbors=1).fit(treated[[X]], treated[Y])
predicted = pd.concat([
# find matches for the treated looking at the untreated knn model
treated.assign(match=mt0.predict(treated[[X]])),
# find matches for the untreated looking at the treated knn model
untreated.assign(match=mt1.predict(untreated[[X]]))
])
predicted.head()
#성향점수 매칭 결과로 얻는 ATE
match_ATE = np.mean((predicted[Y] - predicted["match"])*predicted[T]
+ (predicted["match"] - predicted[Y])*(1-predicted[T]))
print("ATE:", match_ATE)
ATE: -0.34274
역확률 가중치도 동일하게 진행했습니다.
g_data = (data_ps
.assign(
weight = data_ps["Intervention"]/data_ps["propensity_score"] + (1-data_ps["Intervention"])/(1-data_ps["propensity_score"]),
propensity_score=data_ps["propensity_score"].round(2)
)
.groupby(["propensity_score", "Intervention"])
[["weight", "Infant_Mortality_Rate"]]
.mean()
.reset_index())
plt.figure(figsize=(10,4))
for t in [0, 1]:
sns.scatterplot(data=g_data.query(f"Intervention=={t}"), y="Infant_Mortality_Rate", x="propensity_score", size="weight",
sizes=(1,100), color=color[t], legend=None, label=f"T={t}", marker=marker[t])
plt.title("Inverse Probability of Treatment Weighting")
plt.legend()
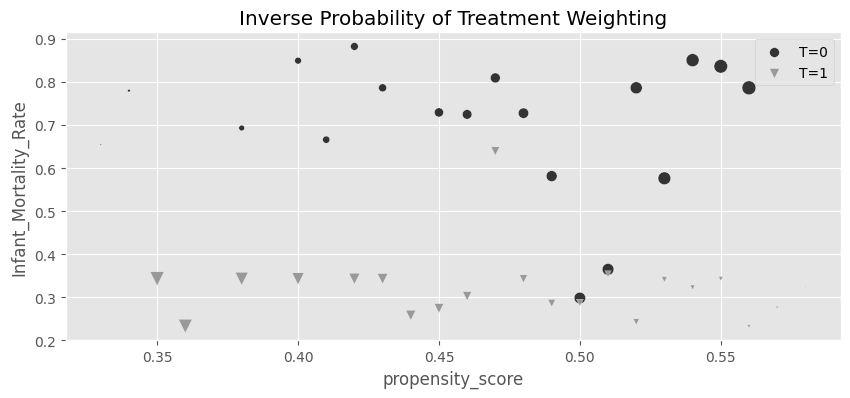
weight_t = 1/data_ps.query("Intervention==1")["propensity_score"]
weight_nt = 1/(1-data_ps.query("Intervention==0")["propensity_score"])
t1 = data_ps.query("Intervention==1")["Infant_Mortality_Rate"]
t0 = data_ps.query("Intervention==0")["Infant_Mortality_Rate"]
y1 = sum(t1*weight_t)/len(data_ps)
y0 = sum(t0*weight_nt)/len(data_ps)
print("E[Y1]:", y1)
print("E[Y0]:", y0)
print("ATE", y1 - y0)
E[Y1]: 0.33483259887812195 E[Y0]: 0.7138347022578627 ATE -0.3790021033797408
#역확률 가중치로 얻는 ATE
IPW_ATE = np.mean(data_ps["Infant_Mortality_Rate"]
* (data_ps["Intervention"] - data_ps["propensity_score"])
/ (data_ps["propensity_score"]*(1-data_ps["propensity_score"])))
print("ATE:",IPW_ATE)
ATE: -0.3790021033797407
각각 도출된 ATE의 경우 이상치를 하나로 진행해서 큰 차이가 없이 둘다 비슷한 크기로 줄어들었습니다. 하지만 학습한 개념으로 미루어보았을 때 역확률 가중치가 더욱 효과적일 것 같습니다. 왜냐하면 역확률 가중는가 각 관측치에 가중치를 부여하여 처리 효과를 추정하기 때문입니다.
반면, 성향점수 매칭은 이상치에 민감할 수 있습니다. 훈련 데이터에 없던 집단의 입풋이 생길 경우 이상치와 매칭 될 수 있는 위험이 있기 때문입니다.
따라서, 데이터에 이상치가 포함되어 있을 경우, 역확률 가중치 방법을 사용하는 것이 더 적절할 것 같습니다.
댓글